An icosahedron based method for even binning of globally distributed remote sensing data
A new scheme is presented for binning globally distributed measurements. The scheme is based on a network of evenly distributed grid points, defined by repeated subdivision of a spherical icosahedron. Delanuany triangulation is then used to obtain bin perimeters for each grid point, which results in a network of bins that are evenly distributed across the entire globe and have uniform area. A modified winding rule is used to determine which datapoints are in which bin. This binning method is especially suited to remote sensing applications involving datasets covering polar regions, where conventional rectangular latitude/longitude bins introduce distortion and streaking into the binned data if noise is present. It also has the property that adjacent bins overlap, providing Nyquist sampling and preventing spatial aliasing. Tests on synthetic data show that this icosahedral binning scheme preserves underlying data trends and is robust to noise.
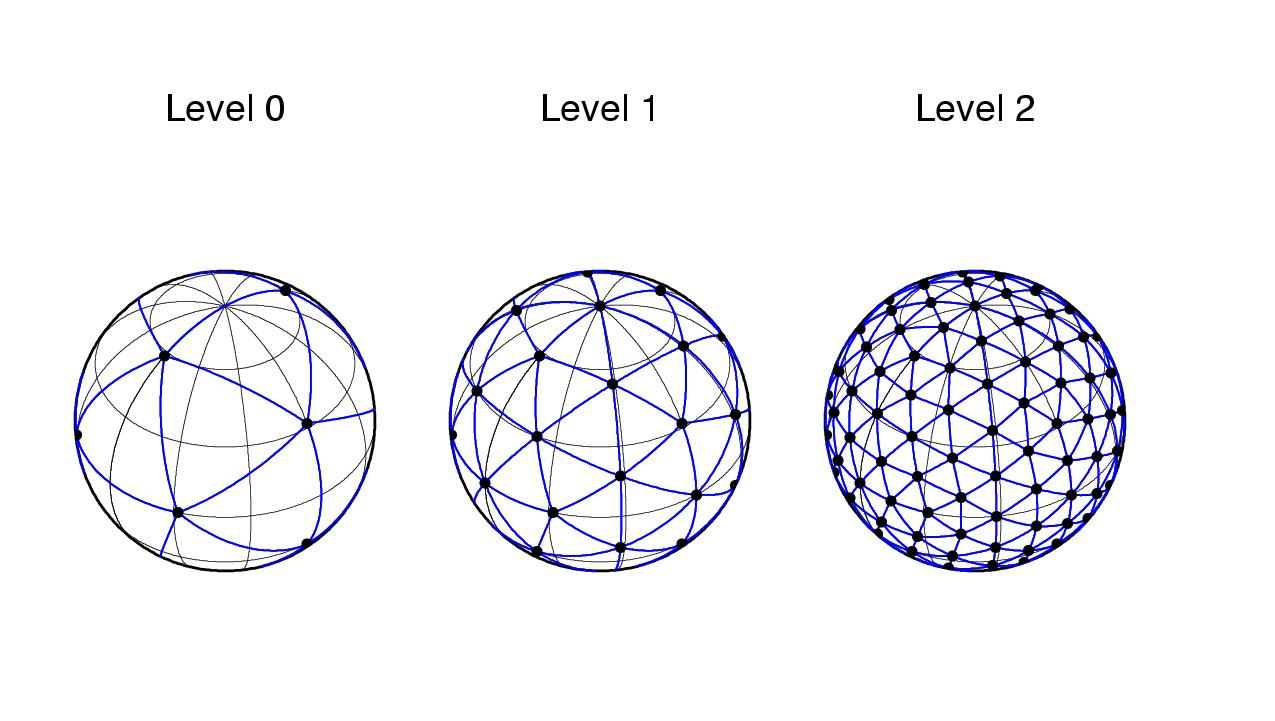
FIG 1. Icosahedral gridding scheme.
N. A. Teanby (2006)
"An icosahedron-based method for even binning of globally distributed remote sensing data"
COMPUTERS & GEOSCIENCES, 32 (9), 1442-1450.
Download PDF from publisher: PDF
Download code (IDL, tar archive): icosahedral binning
Constrained Smoothing of Noisy Data Using Splines in Tension
A method of fitting a smooth cubic spline curve through noisy data points is presented.
Overshoots of the the spline curve between data points were prevented by applying tension to the fit using a quadratic spring approximation, which allowed a linear inverse theory approach to be adopted.
Error-bars in the measured data were mapped through the inversion process to give the covariance of the fitted curve.
This is an improvement over previous methods, which largely neglect the effect of data errors on the fit.
Another improvement is to impose fixed constraints on the fit by simultaneously applying the method of Lagrange multipliers.
The effect of these constraints on the covariance of the fitted curve is quantified using results from linear algebra.
Example applications to synthetic data and a record of magnetic inclination from Hawaii are given.
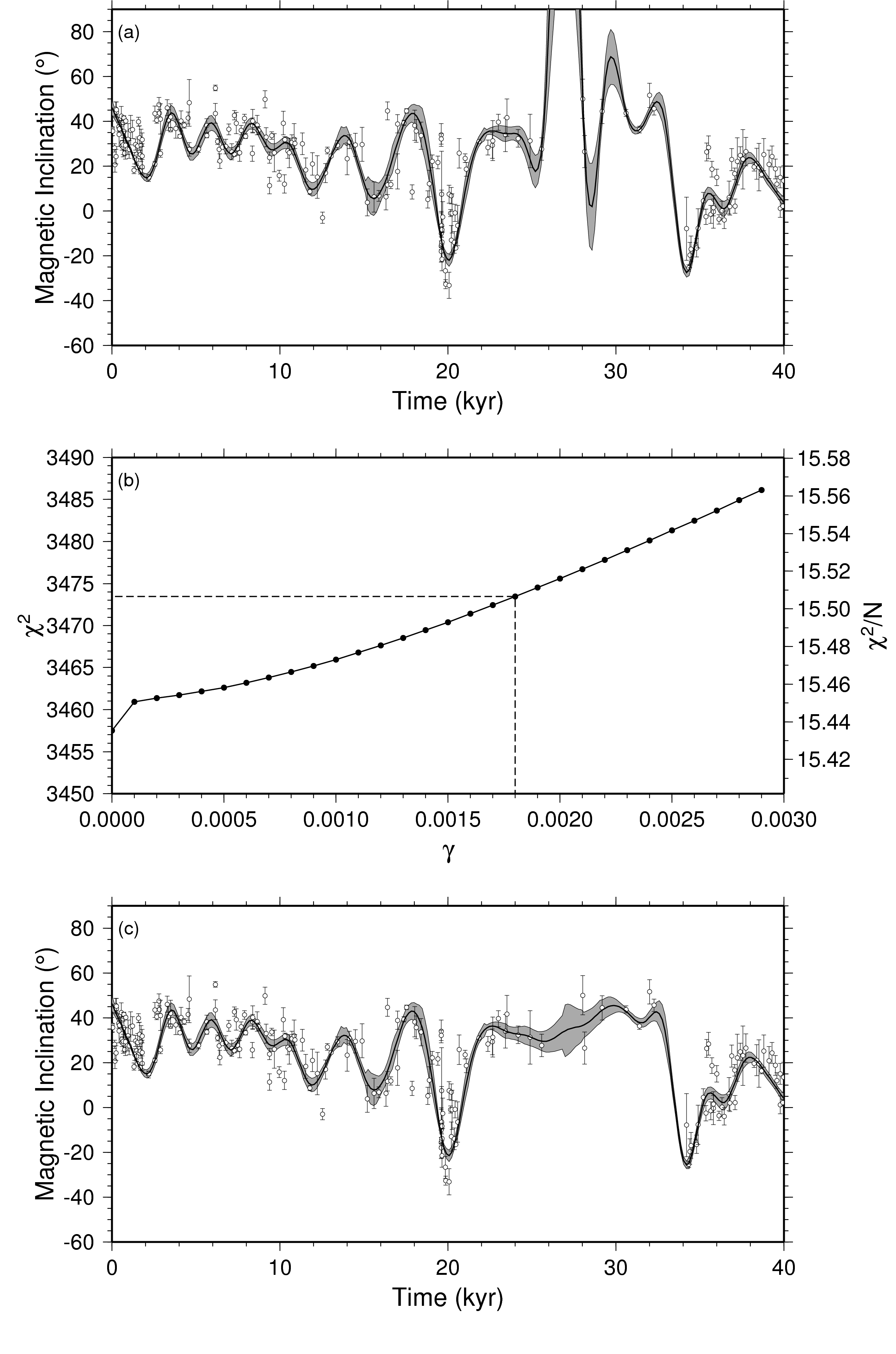
FIG 1. (a) Cubic spline fit of the Hawaiian magnetic inclination record from Teanby et al (2002) with zero tension. The curve fits the data very well, except from 25-34 kyr, where there are large overshoots caused by the sparse data coverage. (b) Shows the effect of increasing the tension gamma on the chi-squared statistic. In (c) a tension of gamma=0.0018 has been applied (see text for criteria), which has corrected the overshoots and preserved the fit elsewhere. The number of parameters M=37 in each case and the grey error envelope has been scaled to account for un-modelled error sources..
N. A. Teanby (2007)
"Smoothing Noisy Data Using Splines in Tension"
Mathematical Geology, 39 (4), 419-434.
Download PDF from publisher: PDF
Download code (Matlab, tar archive): splines